Processing: 2点を通る直線と円の交点を求めよう
目標
今回は以下のようにある2点を通る直線と円の交点を求めるgetCrossPoints()という関数を作ります．
//交点を取得する関数 PVector[] getCrossPoints(float x1, float y1, float x2, float y2, float circleX, float circleY, float r) { //ax + by + c = 0 の定数項 float a = y2-y1; float b = x1-x2; float c = -a*x1-b*y1; //円の中心から直線までの距離 //mag(a, b) = √a^2+b^2 float d = abs((a*circleX+b*circleY+c)/mag(a, b)); //直線の垂線とX軸と平行な線がなす角度θ float theta = atan2(b, a); if (d > r) { return null; } else if (d == r) { PVector[] point = new PVector[1]; //場合わけ if (a*circleX+b*circleY+c > 0)theta += PI; float crossX = r*cos(theta)+circleX; float crossY = r*sin(theta)+circleY; point[0] = new PVector(crossX, crossY); return point; } else { PVector[] crossPoint = new PVector[2]; float[]crossX = new float[2]; float[]crossY = new float[2]; //alphaとbetaの角度を求める float alpha, beta, phi; phi = acos(d/r); alpha = theta - phi; beta = theta + phi; //場合わけ if (a*circleX+b*circleY+c > 0) { alpha += PI; beta += PI; } //交点の座標を求める crossX[0] = r*cos(alpha) + circleX; crossY[0] = r*sin(alpha) + circleY; crossX[1] = r*cos(beta) + circleX; crossY[1] = r*sin(beta) + circleY; for (int i = 0; i < crossPoint.length; i++) crossPoint[i] = new PVector(crossX[i], crossY[i]); return crossPoint; } }
動画のプログラムは，こちらを実行すれば体験できます．
2点を通る直線と円の交点の求め方
ここからは直線と円の交点をどうやって求めているのか解説したいと思います
直線と円の交点があるかを確認
まず「直線と円が交わっているのか？」を確認しないといけません．
確認の方法は至って簡単で，直線と円の中心の距離をdとしたときに，r < dだったら直線が円から離れているので交わっていません．
r = dのときはちょうど円と直線が接しています．そして，r > dだったら直線と円は2つの交点を持ちます．
dの求め方
dは点と直線の距離の公式を使うことで，求めることが可能です．
点(
, 
)と直線(
)の距離の公式
コードにすると……
//円の中心から直線までの距離 //mag(a, b) = √a^2+b^2 float d = abs((a*circleX+b*circleY+c)/mag(a, b)); if (d > r) { //交点が0のとき }else if (d == r) { //交点が1つのとき }else{ //交点が2つのとき }
直線と円が接しているとき
まず直線と円が接しているときに交点の座標をどのように求めるのかを解説していきます．
交点の座標の求め方
例えば円の中心が原点だったときのことを考えます．
円と直線の距離をdとし，直線の垂線がX軸と平行な線となす角をθとすると交点の座標は
float x = r*cos(theta); float y = r*sin(theta);
となります．
円の中心が(centerX, centerY)だった場合は平行移動させればいいので
float x = r*cos(theta) + centerX; float y = r*sin(theta) + centerY;
とすれば，交点の座標を求めることができます．
θの求め方
直線と円との距離は，円の半径と同じであるため求めるのが簡単です．一方，θの値はどうやって求めればいいのでしょうか．
円と接する直線の方程式をax + by + c = 0とすると，その垂線の傾きはb/aとなることが知られています．
そして，傾きはtan()を使って表すこともでき，tan(θ) = b/aとなります．
これを満たすθを求める命令がatan2()です．
float theta = atan2(b, a);
これでθの値を求めることができました．
atan2()の罠
先ほど紹介したθの求め方だけだと，正しい交点の座標を求めることはできません．それは．θの値を直線の方程式のaとbを使うことで角度を求めているので，その値に円と直線の位置関係が反映されていないからです．
これは，a*centerX + b*centerY + cが0より大きいか小さいかで場合わけすることで対処することができます（理由は後日記述します）．
float theta = atan2(b, a); if (a*circleX+b*circleY+c > 0) theta += PI;
このようにa*circleX+b*circleY+c > 0のときにθに180°足すと，円と直線の位置関係が反映されて，正しい交点の座標を求めることができます．
コードにすると……
これまで説明したことをコードにすると以下のようになります．
float theta = atan2(b, a); //場合わけ if (a*circleX+b*circleY+c > 0)theta += PI; float crossX = r*cos(theta)+circleX; float crossY = r*sin(theta)+circleY;
直線と円の交点が2つのとき
次に直線と円の交点が2つのときに交点の座標をどのように求めるのかを解説していきます．
交点の座標の求め方
直線と円が接しているときと同じ考え方で求めます．円の中心と交点を通る直線とX軸と平行な線のなす角をそれぞれα, βとすると
float crossX1 = r*cos(alpha) + centerX; float crossY1 = r*sin(alpha) + centerY; float crossX2 = r*cos(beta) + centerX; float crossY2 = r*sin(beta) + centerY;
として求めることができます．
αとβの求め方
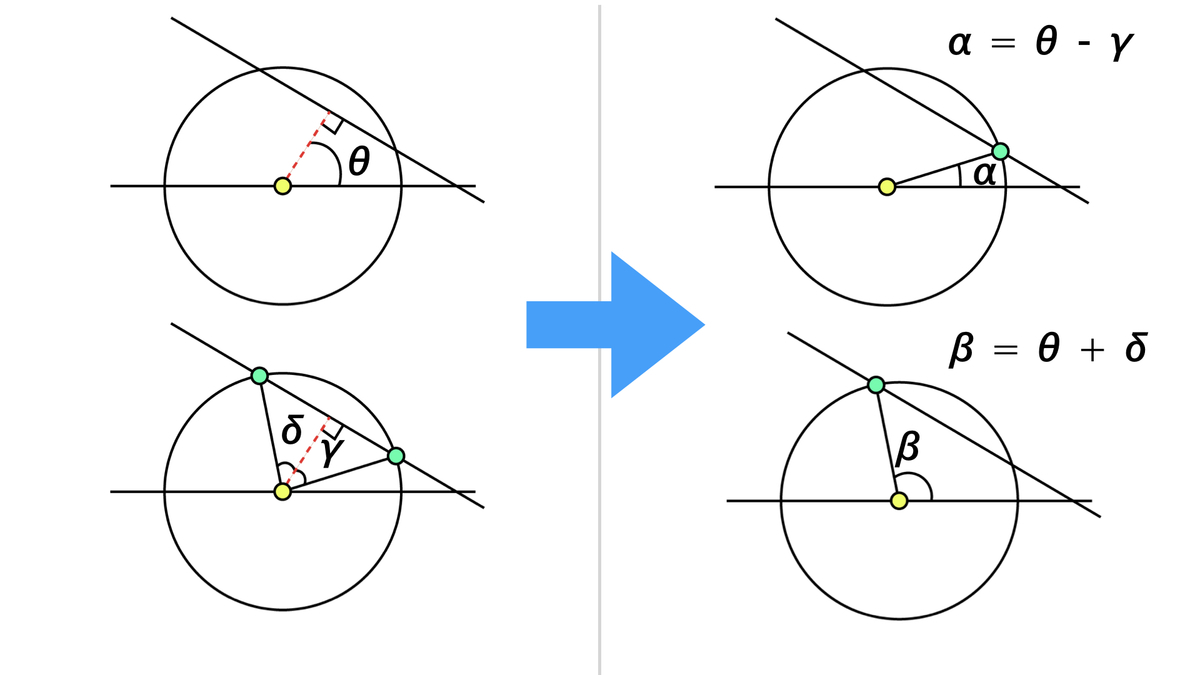直線の垂線AがX軸と平行な線となす角をθとし，「円の中心を通る垂線A」が「円の中心と交点を通る直線B, C」となす角をそれぞれγ，δとすると
float alpha = theta - gamma; float beta = theta + delta;
として求めることができます．
γ，δの求め方
「円の中心と交点の直線」と「円の中心から直線の垂線」を引きます．
そしてできた直角三角形を見てみると，それぞれ合同であることが分かります．
つまり，φ = γ = δとなるφの値を求めるだけで済みます．
直角三角形であることを利用すればφを求めることは簡単です．
r, d, φは，cos(φ) = d/rという関係があります．
これはatan()のときと同じようにacos()という命令を使えば，求めることが可能です．
float phi = acos(d/r);
これでphiの値を求めることができました．
コードにすると……
これまで説明したことをコードにすると以下のようになります．
（atan2()の場合わけも忘れないように！）
phi = acos(d/r); alpha = theta - phi; beta = theta + phi; //場合わけ if (a*circleX+b*circleY+c > 0) { alpha += PI; beta += PI; } //交点の座標を求める crossX[0] = r*cos(alpha) + circleX; crossY[0] = r*sin(alpha) + circleY; crossX[1] = r*cos(beta) + circleX; crossY[1] = r*sin(beta) + circleY;
おわりに
今回は，2点を通る直線と円の交点の求め方について解説しました．この記事の知識をプログラム作品に応用してもらえたら幸いです．
